Выделение в метод последовательной части конечного автомата
Во многих конечных автоматах встречаются последовательные части - несколько состояний, вытянутых в цепочку, с одним входом и одним выходом для каждого состояния (). Согласно исследованию, проведённому в [], 25 % рассмотренных крупных автоматов содержат последовательные цепочки длинной 3 и более состояний.
В таких ситуациях все состояния, входящие в цепочку, можно перенести в метод. Это позволит упростить общий вид конечного автомата, уменьшить количество состояний и переходов и скрыть детали поведения автомата при последовательном прохождении нескольких состояний. Назовём такую трансформацию «выделением в метод последовательной части конечного автомата».
В результате применения трансформации «Выделение метода», создаётся метод Proc () с реализацией в виде конечного автомата ().
Все состояния из последовательной цепочки состояний (в данном примере X, Y и Z) переносятся в выделенный метод. Последний переход цепочки состояний, перенесённый в метод, завершается возвратом из метода (return). Действия, приписанные началу цепочки переходов, становятся действиями, приписанными начальному переходу конечного автомата метода Proc (). Вместо них в исходный конечный автомат вставляются вызов метода Proc () и команда перехода в состояние, следующее за цепочкой (Q) (Рис. 7)
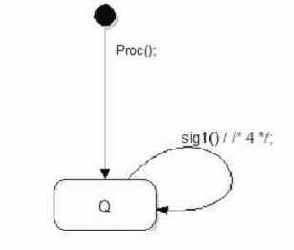
Рис. 7. Результат трансформации
Последовательные цепочки состояний, используемые в конечных автоматах, являются неким многошаговым переходом, определяющим последовательность действий и состояний, которые необходимо пройти, чтобы попасть в очередную часть автомата. Таким образом, все состояния и переходы, формирующие цепочку, являются логически связанными и допускают группировку в отдельную структурную единицу автомата - метод.
