Теория графов
Граф можно рассматривать как графическую нотацию для бинарного отношения двух множеств. Бинарное отношение состоит из таких кортежей или списков элементов, которые содержат только два элемента некоторого множества. Хотя основные понятия теории графов получили свое развитие задолго до появления теории множеств как самостоятельной научной дисциплины, формальное определение графа удобно представить в теоретико-множественных терминах.
Графом называется совокупность двух множеств: множества точек или вершин и множества соединяющих их линий или ребер. Формально граф задается в виде двух множеств: G=(V, Е), где V={v1v2, ..., vn} — множество вершин графа, а Е={е1, е2, ..., еm} — множество ребер графа. Натуральное число n определяет общее количество вершин конкретного графа, а натуральное число m — общее количество ребер графа. Следует заметить, в общем случае не все вершины графа могут соединяться между собой, что ставит в соответствие каждому графу некоторое бинарное отношение PQ, состоящее из всех пар вида <vi, vj>, где vi, vj = V. При этом пара <vi, vj> и, соответственно, пара <vj, vi> принадлежат отношению PG в том и только в том случае, если вершины vi и vj соединяются в графе G некоторым ребром ek=Е. Вершины графа изображаются точками, а ребра — отрезками прямых линий. Рядом с вершинами и ребрами записываются соответствующие номера или идентификаторы, позволяющие их идентифицировать однозначным образом.
Примечание
Вообще говоря, графы бывают двух различных типов. Рассмотренное выше определение относится к неориентированному графу, т. е. к такому графу, у которого связывающие вершины ребра не имеют направления или ориентации. Кроме неориентированных графов существуют ориентированные графы, которые определяются следующим образом.
Ориентированный граф также задается в виде двух множеств G=(V, E), где V={v1, v2, ...,vn} — множество вершин графа, а E={е1, е2,...,еm] — множество дуг графа. Натуральное число n определяет общее количество вершин конкретного графа, а натуральное число m — общее количество дуг графа.
При этом каждая дуга еk=Е ориентированного графа G имеет свое начало— некоторую единственную вершину vi=V и конец — некоторую единственную вершину vj=V, В отличие от ребра, дуга всегда имеет обозначение со стрелочкой, которая направлена к конечной вершине дуги. Множество дуг ставит в соответствие каждому ориентированному графу некоторое бинарное отношение PG, состоящее из всех пар вида <vi, vj>, где vi, vj=V. При этом пара <vi, vj> принадлежит отношению PG в том и только в том случае, если вершины vi и vj соединяются в графе G некоторой дугой еk=Е с началом в вершине viи концом в вершине vj.
Ниже представлены два примера конкретных графов (рис. 2.4). При этом первый из них (рис. 2.4, а) является неориентированным графом, а второй (рис. 2.4, б) — ориентированным графом. Как нетрудно заметить, для неориентированного графа ребро е1 соединяет вершины v1 и v2, ребро е2 — вершины v1 и v3, а ребро e3 — вершины v2 и v3 и т. д. Последнее ребро, e8, соединяет вершины v4 и v5, тем самым задается описание графа в целом. Других ребер данный граф не содержит, как не содержит других вершин, не изображенных на рисунке. Так, хотя ребра е6 и e7 визуально пересекаются, но точка их пересечения не является вершиной графа.
Для ориентированного графа (рис. 2.4, б) ситуация несколько иная. А именно, вершины v1 и v2 соединены дугой е1, для которой вершина v2 является началом дуги, а вершина v1 — концом этой дуги. Далее дуга е2 соединяет вершины v1 и v4, при этом началом дуги e2
является вершина v1, а концом — вершина v4.
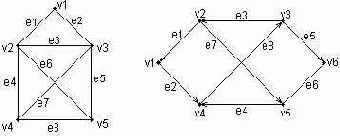
Рис. 2.4. Примеры неориентированного (а) и ориентированного (б) графов
Графы широко применяются для представления различной информации о структуре систем и процессов. Примерами подобных графических моделей могут служить: схемы автомобильных дорог, соединяющих отдельные населенные пункты; схемы телекоммуникаций, используемых для передачи информации между отдельными узлами; схемы программ, на которых указываются варианты ветвления вычислительного процесса.
Общим для всех конкретных подобных моделей является возможность представления информации в графическом виде в форме соответствующего графа. При этом отдельные модели, как правило, обладают дополнительной семантикой и специальными обозначениями, характерными для той или иной предметной области.
Важными понятиями теории графов являются понятия маршрута и пути, которые ассоциируются с последовательным перемещением от вершины к вершине по соединяющим их ребрам или дугам. Для неориентированного графа маршрут определяется как конечная или бесконечная упорядоченная последовательность ребер S=<, esl, es2, ..., esk>>, таких, что каждые два соседних ребра имеют общую вершину. Нас будут интересовать только конечные маршруты S=<es1, es2, ..., esk>, т. е. такие маршруты, которые состоят из конечного числа ребер. При этом ребро esl принято считать началом маршрута S, а ребро esk — концом маршрута S. Для ориентированного графа соответствующая последовательность дуг S=<es1, es2, ..., esk> называется ориентированным маршрутом, если две соседние дуги имеют общую вершину, которая является концом предыдущей и началом последующей дуги.
Примерами маршрутов для неориентированного графа (рис. 2.4, а) являются последовательности ребер: S1=<e1, e2 e5, e8>, S2=<e1, e2, е3, e1>, S3=<e3, e5, e8>. Если в маршруте не повторяются ни ребра, ни вершины, как в случае S1 и S3, то такой неориентированный маршрут называется простой цепью.
Примерами ориентированных маршрутов для графа (рис. 2.4, б) являются такие последовательности дуг: S1=<e2, e8, e5>, S2=<e3, e7, e6>, S3=<e8, e3, e7, e4, e8>. Если в ориентированном маршруте не повторяются ни ребра, ни вершины, как в случае S1 и S2, то такой ориентированный маршрут называется путем. Последнее понятие также иногда применяется для обозначения простой цепи в неориентированных графах и для определения специального класса графов, так называемых деревьев. В общем случае деревья служат для графического представления иерархических структур или иерархий, занимающих важное место в ООАП.
Деревом в теории графов называется такой граф D=<V, E>, между любыми двумя вершинами которого существует единственная простая цепь, т. е. неориентированный маршрут, у которого вершины и ребра не повторяются. Применительно к ориентированным графам соответствующее определение является более сложным, поскольку основывается на выделении некоторой специальной вершины v0, которая получила специальное название корневой вершины или просто — корня. В этом случае ориентированный граф D=<V, Е> называется ориентированным деревом или сокращенно — деревом, если между корнем дерева v0 и любой другой вершиной существует единственный путь, берущий начало в v0. Ниже представлены два примера деревьев: неориентированного дерева (рис. 2.5, а) и ориентированного дерева (рис. 2.5, б).
В случае неориентированного дерева (рис. 2.5, а) любая из вершин графа может быть выбрана в качестве корня. Подобный выбор определяется специфическими особенностями решаемой задачи. Так, вершина v1 может рассматриваться в качестве корня неориентированного дерева, поскольку между v1 и любой другой вершиной дерева всегда существует единственная простая цепь по определению (или, что менее строго, единственный неориентированный путь).
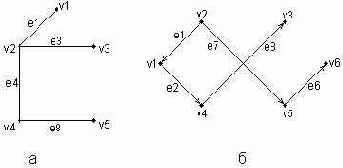
Рис. 2.5. Примеры неориентированного (а) и ориентированного (б) деревьев
Для случая ориентированного дерева (рис. 2.5, б) вершина v2 является единственным его корнем и имеет специальное обозначение v0. Единственность корня в ориентированном дереве следует из того факта, что ориентированный путь всегда имеет единственную вершину, которая является его началом. Поскольку в теории графов имеет значение только наличие или отсутствие связей между отдельными вершинами, деревья, как правило, изображаются специальным образом в виде иерархической структуры. При этом корень дерева изображается самой верхней вершиной в данной иерархии. Далее следуют вершины уровня 1, которые связаны с корнем одним ребром или одной дугой. Следующий уровень будет иметь номер 2, поскольку соответствующие вершины должны быть связаны с корнем двумя последовательными ребрами или дугами.
Процесс построения иерархического дерева продолжается до тех пор, пока не будут рассмотрены вершины, которые не связаны с другими вершинами, кроме рассмотренных, или из которых не выходит ни одна дуга. В этом случае самые нижние вершины иногда называют листьями дерева. Важно иметь в виду, что в теории графов дерево "растет" вниз, а не вверх, как в реальной жизни.
Изображенные выше деревья (рис. 2.5) можно преобразовать к виду иерархий. Например, неориентированное дерево (рис. 2.5, а) может быть представлено в виде иерархического дерева следующим образом (рис. 2.6, а). В этом случае корнем иерархии является вершина v1. Ориентированное дерево (рис. 2.5, б) также может быть изображено в форме иерархического дерева (рис. 2.6, б), однако такое представление является единственным.
В первом случае (рис. 2.6, а) вершина v2 образует первый уровень иерархии, вершины v4 и v3 — второй уровень иерархии, вершина v5 — третий и последний уровень иерархии. При этом листьями данного неориентированного дерева являются вершины v3 и v5. Во втором случае (рис. 2.6, б) вершины v1 и v5 образуют первый уровень иерархии, вершины v4 и v6 — второй уровень иерархии, вершина v3 — третий и последний уровень иерархии. Листьями данного ориентированного дерева являются вершины v3 и v6.
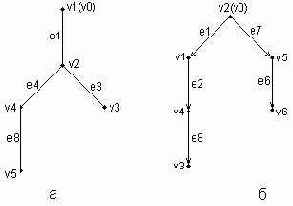
Рис. 2.6. Иерархические схемы неориентированного дерева (а) и ориентированного дерева (б)
В заключение следует заметить, что в теории графов разработаны различные методы анализа отдельных классов графов и алгоритмы построения специальных графических объектов, рассмотрение которых выходит за рамки настоящей книги. Для получения дополнительной информации по данной теме можно рекомендовать обратиться к специальной литературе по теории графов, где эти вопросы рассмотрены более подробно. В дальнейшем нас будет интересовать отдельное направление в теории графов, которое связано с явным включением семантики в традиционные обозначения и получившее самостоятельное развитие в форме семантических сетей.