Теория множеств
Как одну из наиболее известных систем графических символов, оказавших непосредственное влияние на развитие научного мышления, следует отметить язык диаграмм английского логика Джона Венна (1834—1923). В настоящее время диаграммы Венна применяются для иллюстрации основных теоретико-множественных операций, которые являются предметом специального раздела математики — теории множеств. Поскольку многие общие идеи моделирования систем имеют адекватное описание в терминологии теории множеств, рассмотрим основные понятия данной теории, имеющие отношение к современным концепциям и технологиям исследования сложных систем.
Исходным понятием теории множеств является само понятие множество, под которым принято понимать некоторую совокупность объектов, хорошо различимых нашей мыслью или интуицией. При этом не делается никаких предположений ни о природе этих объектов, ни о способе их включения в данную совокупность. Отдельные объекты, составляющие то или иное множество, называют элементами данного множества. Вопрос "Почему мы рассматриваем ту или иную совокупность элементов как множество?" не требует ответа, поскольку в общее определение множества не входят никакие дополнительные условия на включение отдельных элементов в множество. Если нам хочется, например, рассмотреть множество, состоящее из трех элементов: "солнце, море, апельсин", то никто не сможет запретить это сделать.
Примеров конкретных множеств можно привести достаточно много. Это и множество квартир жилого дома, и множество натуральных чисел, с которого начинается знакомство каждого ребенка с великим таинством счета. Совокупность компьютеров в офисе тоже представляет собой множество, хотя, возможно, они и соединены между собою в сеть. Множество живущих на планете людей, как и множество звезд на небосводе, тоже могут служить примерами множеств, хотя природа их существенно различна.
Примечание
Создается впечатление, что ситуация с заданием множеств более или менее понятна. Но это впечатление обманчиво.
Даже не говоря об известных парадоксах теории множеств, как быть с "множеством" мыслей отдельного человека? Или множеством всех красок, которые встречаются в природе? Однако такие каверзные случаи мы рассматривать не будем, ограничив круг ситуаций такими, в которых идентификация отдельных элементов множеств не превращается в серьезную проблему. С другой стороны, процесс моделирования сложных систем сопряжен именно с подобного рода трудностями.
В теории множеств используется специальное соглашение, по которому множества обозначаются прописными буквами латинского алфавита, и традиция эта настолько общепризнана, что не возникает никакого сомнения в ее целесообразности. При этом отдельные элементы обозначаются строчными буквами, иногда с индексами, которые вносят некоторую упорядоченность в последовательность рассмотрения этих элементов. Важно понимать, что какой бы то ни было порядок, вообще говоря, не входит в исходное определение множества. Таким образом, множество, например, квартир 100-квартирного жилого дома с использованием специальных обозначений можно записать следующим образом: A={aj, 02, а3, ..., а{00}. Здесь фигурные скобки служат обозначением совокупности элементов, каждый из которых имеет свой уникальный числовой индекс. Важно понимать, что для данного конкретного множества элемент ato обозначает отдельную квартиру в рассматриваемом жилом доме. При этом вовсе необязательно, чтобы номер этой квартиры был равен 10, хотя с точки зрения удобства это было бы желательно.
Принято называть элементы отдельного множества принадлежащими данному множеству. Данный факт записывается при помощи специального символа "е", который так и называется — символ принадлежности. Например, запись а10ьА означает тот простой факт, что отдельная квартира (возможно, с номером 10) принадлежит рассматриваемому множеству квартир некоторого жилого дома.
Следующим важным понятием, которое служит прототипом многих более конкретных терминов при моделировании сложных систем, является понятие подмножества.
Казалось бы, интуитивно и здесь нет ничего неясного. Если есть некоторая совокупность, рассматриваемая как множество, то любая ее часть и будет являться подмножеством. Так, например, совокупность квартир на первом этаже жилого дома есть ничто иное, как подмножество рассматриваемого нами примера. Ситуация становится не столь тривиальной, если рассматривать множество абстрактных понятий, таких как сущность или класс.
Для обозначения подмножества используется специальный символ. Если утверждается, что множество А является подмножеством множества В, то это записывается как Аа В. Запоминать подобные значки не всегда удобно, поэтому со временем была предложена специальная система графических обозначений.
Как же используются диаграммы Венна в теории множеств? Оказывается, тот факт, что некоторая совокупность элементов образует множество, можно обозначить графически в виде круга. В этом случае окружность имеет содержательный смысл или, выражаясь более точным языком, семантику границы данного множества. Очевидно, что рассмотрение отношения включения элементов одного множества в другое можно изобразить графически следующим образом (рис. 2.1). На этом рисунке большему множеству В соответствует внешний круг, а меньшему множеству (подмножеству) А — внутренний.
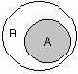
Рис. 2.1. Диаграмма Венна для отношения включения двух множеств
Подобным образом можно изобразить и основные теоретико-множественные операции. Так, пересечением двух множеств А и В называется некоторое третье множество С, которое состоит из тех и только тех элементов двух исходных множеств, которые одновременно принадлежат и множеству А, и множеству В. Для этой операции также имеется специальное обозначение: С= А о В. Например, если в качестве множества А для операции пересечения рассмотреть множество сотрудников некоторой фирмы, а в качестве множества В — множество всех мужчин, то нетрудно догадаться, что множество С будет состоять из элементов -± всех сотрудников мужского пола данной фирмы. Операция пересечения множеств также может быть проиллюстрирована с помощью диаграмм Венна (рис. 2.2).
На этом рисунке условно изображены два множества А и В, затененной области как раз и соответствует множество С, являющееся пересечением множеств А и В.
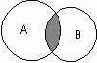
Рис. 2.2 Диаграмма Венна для пересечения двух множеств
Следующей операцией, которая также допускает наглядную интерпретацию, является операция объединения множеств. Под объединением двух множеств А и В понимается некоторое третье множество, пусть это будет D, которое состоит из тех и только тех элементов, которые принадлежат или А, или В, или им обоим одновременно. Конечно, специальное обозначение есть и для этой операции: D= AuB. Так, если в качестве множества А рассмотреть множество, состоящее из клавиатуры и мыши, а в качестве множества В — множество, состоящее из системного блока и монитора, то нетрудно догадаться, что их объединение, т. е. множество D, образует основные составляющие персонального компьютера. И для этой операции имеется условное графическое представление (рис. 2.3). На этом рисунке объединению двух исходных множеств также соответствует затемненная область, только размеры и форма ее отличаются от случая пересечения двух множеств на предыдущем рисунке.
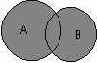
Рис. 2.3. Диаграмма Венна для объединения двух множеств
Примечание
При выборе обозначений для множеств допускается некоторый произвол, который не всегда понятен лицам, далеким от математики. Однако здесь уместна аналогия с выбором имен для переменных и процедур в языках высокого уровня, когда программист сам решает, как ему обозначать соответствующую конструкцию в программе.
Последнее, на что следовало бы обратить внимание при столь кратком знакомстве с основами теории множеств — это на так называемые понятия мощности множества и отношения множеств. Хотя существуют и другие операции над множествами, а также целый ряд дополнительных понятий, их рассмотрение выходит за рамки настоящей книги. Что касается понятия мощности множества, то данный термин важен для анализа кратности связей, поскольку ассоциируется с количеством элементов отдельного множества.
В случае конечного множества ситуация очень простая, поскольку мощность конечного множества равна количеству элементов этого множества. Таким образом, возвращаясь к примеру с множеством А квартир жилого дома, можно сказать, что его мощность равна 100.
Ситуация усложняется, когда рассматриваются бесконечные множества, т. е. множества, не являющиеся конечными. Не вдаваясь в технические детали, которые послужили источником драматичного по своим последствиям кризиса основ математики, ограничим наше рассмотрение бесконечными множествами счетной мощности. Такими множествами принято считать множества, содержащие бесконечное число элементов, которые, однако, можно перенумеровать натуральными числами 1, 2, 3 и т. д. При этом важно иметь в виду, что достичь последнего элемента при такой нумерации принципиально невозможно, иначе множество окажется конечным. Например, есть все основания считать множество всех звезд бесконечным, хотя многие из них имеют свое уникальное название. С другой стороны, множество всех возможных комбинаций из 8 символов, которые могут служить для ввода некоторого пароля, конечное, хотя и достаточно большое. Или, говоря строгим языком, это множество имеет конечную мощность.
Примечание
Проблема бесконечного могла бы показаться отвлеченной и имеющей некоторый философский оттенок, если бы не ее связь с моделированием сложных систем. Так, при рассмотрении некоторой предметной области с целью построения ее модели приходится выделять конечное число сущностей, образующих определенный "скелет" будущей модели. И это при том, что реальность предметов допускает бесконечное рассмотрение их свойств, атрибутов и взаимосвязей.
Наконец, было упомянуто и следующее понятие, различные аспекты которого будут служить темой рассмотрения во всех последующих главах. Это фундаментальное понятие отношения множеств, которое часто заменяется терминами связь или соотношение. Данный термин ведет свое происхождение от теории множеств и служит для обозначения любого подмножества упорядоченных кортежей, построенных из элементов некоторых исходных множеств.
При этом под кортежем понимается просто набор или список элементов, важно только, чтобы они были упорядочены. Другими словами, если рассматривать первый элемент кортежа, то он всегда будет первым в списке элементов, второй элемент кортежа будет вторым элементом в списке и т. д. Можно ли это записать с использованием специальных обозначений?
Хотя и существует некоторая неоднозначность в принятых обозначениях, кортеж из двух элементов удобно обозначать как <a1, a2>, из трех элементов — <a1, a2, a3> и т. д. При этом отдельные элементы могут принадлежать как одному и тому же множеству, так и различным множествам. Важно иметь в виду, что порядок выбора элементов для построения кортежей строго фиксирован для конкретной задачи. Речь идет о том, что первый элемент всегда выбирается из первого множества, второй — из второго, и т. д:
Отношение в этом случае будет характеризовать способ или семантику выбора отдельных элементов из одного или нескольких множеств для подобного упорядоченного списка. В этом смысле взаимосвязь является частным случаем отношения, о чем будет сказано в последующем. К сожалению, диаграммы Венна не предназначены для иллюстрации отношений в общем случае. Однако отношения послужили исходной идеей для развития другой теории, которая даже в своем названии несет отпечаток графической нотации, а именно — теории графов. В этой связи наиболее важным является тот факт, что теоретико-множественные отношения послужили также основой для разработки реляционной алгебры в теории реляционных баз данных. Развитие последней привело к тому, что в последние годы именно реляционные СУБД конкретных фирм доминируют на рынке соответствующего программного обеспечения.