Отношение обобщения
Отношение обобщения является обычным таксономическим отношением между более общим элементом (родителем или предком) и более частным или специальным элементом (дочерним или потомком). Данное отношение может использоваться для представления взаимосвязей между пакетами, классами, вариантами использования и другими элементами языка UML.
Применительно к диаграмме классов данное отношение описывает иерархическое строение классов и наследование их свойств и поведения. При этом предполагается, что класс-потомок обладает всеми свойствами и поведением класса-предка, а также имеет свои собственные свойства и поведение, которые отсутствуют у класса-предка. На диаграммах отношение обобщения обозначается сплошной линией с треугольной стрелкой на одном из концов (рис. 5.12). Стрелка указывает на более общий класс (класс-предок или суперкласс), а ее отсутствие — на более специальный класс (класс-потомок или подкласс).

Рис. 5.12. Графическое изображение отношения обобщения в языке UML
Как правило, на диаграмме может указываться несколько линий для одного отношения обобщения, что отражает его таксономический характер. В этом случае более общий класс разбивается на подклассы одним отношением Обобщения. Например, класс Геометрическая_фигура_на_плоскости (курсив обозначает абстрактный класс) может выступать в качестве суперкласса для подклассов, соответствующих конкретным геометрическим фигурам, таким как,Прямоугольник, Окружность, Эллипс и др. Данный факт может быть представлен графически в форме диаграммы классов следующего вида (рис. 5.13).

Рис. 5.13. Пример графического изображения отношения обобщения классов
С целью упрощения обозначений на диаграмме классов совокупность линий, обозначающих одно и то же отношение обобщения, может быть объединена в одну линию. В этом случае данные отдельные линии изображаются сходящимися к единственной .стрелке, имеющей с ними общую точку пересечения (рис. 5.14).
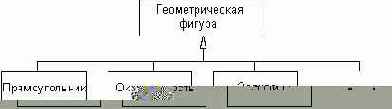
Рис. 5.14. Вариант графического изображения отношения обобщения классов для случая объединения отдельных линий
Это обозначение по форме соответствует графу специального вида, который рассматривался в главе 2, а именно — иерархическому дереву. В этом случае класс-предок является корнем этого дерева, а классы-потомки — его листьями. Отличие заключается в возможности указания на диаграмме классов потенциальной возможности наличия других классов-потомков, которые не включены в обозначения представленных на диаграмме классов (многоточие вместо прямоугольника).
Рядом со стрелкой обобщения может размещаться строка текста, указывающая на некоторые дополнительные свойства этого отношения. Данный текст будет относиться ко всем линиям обобщения, которые идут к классам-потомкам. Другими словами, отмеченное свойство касается всех подклассов данного отношения. При этом текст следует рассматривать как ограничение, и тогда он записывается в фигурных скобках.
В качестве ограничений могут быть использованы следующие ключевые слова языка UML:
С другой стороны, для отдельной задачи, такой как разработка системы продажи автомобилей конкретных моделей, в этом нет необходимости. Но указать неполноту структуры классов-потомков все же следует;
С учетом возможности использования строк-ограничений диаграмма классов (рис. 5.14) может быть изображена без многоточий и без потери информации (рис. 5.15).
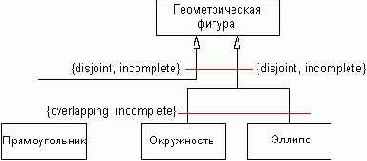
Рис. 5.15. Вариант графического изображения отношения обобщения классов с использованием строки-ограничения
Чтобы проиллюстрировать особенности использования отношения обобщения, преобразуем один из рассмотренных ранее примеров изображения классов в графическую нотацию языка UML. В качестве такого примера рассмотрим иерархию вложенности классов для абстрактного класса "Автомобиль" (см. рис. 1,2, 2.7). Как нетрудно заметить, отношение между отдельными классами на этих рисунках есть именно отношение обобщения, которое в языке UML имеет специальное графическое обозначение. С учетом этой графической нотации, фрагмент семантической сети для представления иерархии класса "Автомобиль" (см. рис. 2.7) может быть представлен в виде следующей диаграммы классов (рис. 5.16).
Заметим, что в данном примере все классы верхних уровней являются абстрактными, т. е. не могут быть представлены своими экземплярами. Именно поэтому их имена записаны курсивом. В отличие от них классы нижнего уровня являются конкретными, поскольку могут быть представлены своими экземплярами, в качестве которых выступают изготовленные автомобили соответствующей модели с уникальным заводским номером.
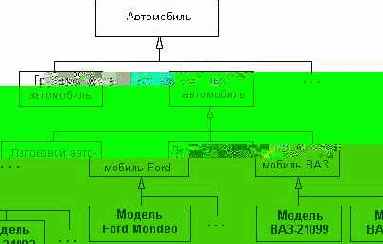
Рис. 5.16. Фрагмент диаграммы классов с отношением обобщения для представления иерархии классов "Автомобиль" из рассмотренного ранее примера (см. рис. 2.7)
Примечание
В качестве упражнения для закрепления рассмотренного материала можно попытаться построить диаграммы классов или хотя бы их фрагменты для библиотек стандартных классов MFC (Microsoft) и VCL (Borland/Inprise) с использованием графической нотации языка UML. Можно предположить, что в недалеком будущем справочные руководства по соответствующим средам програм
Примеры стереотипов для отношения зависимости представлены ниже:
Примечание
Отношение зависимости является наиболее общей формой отношения в языке UML. Все другие типы рассматриваемых отношений можно считать частным случаем данного отношения. Однако важность выделения специфических семантических свойств и дополнительных характеристик для других типов отношений обусловливают их самостоятельное рассмотрение при построении диаграмм.
мирования будут содержать именно такие диаграммы классов, а возможно, и некоторые другие.